

cl-buchberger is a Common Lisp implementation of Buchberger's algorithm for the computation of Groebner bases.
Currently this package can compute Groebner bases of ideals in multivariate polynomial rings over the rationals.
Download the latest version of this package from http://github.com/jmbr/cl-buchberger/tarball/master
The code has been tested under
ABCL 0.16.0-dev
CLISP 2.47
ECL 9.6.1
SBCL 1.0.29
cl-buchberger is released under the GNU GPLv2.
You need ASDF installed in your system. To load cl-buchberger, write:
CL-USER> (asdf:operate 'asdf:load-op :cl-buchberger) NIL CL-USER> (use-package :cl-buchberger) T
There's a default ring which is the ring of polynomials on X, Y, Z over the rationals. To define custom polynomial rings use:
CL-USER> (make-instance 'polynomial-ring :variables
(list 'x 'y 'z 'u 'w 'r 's 't))
#<POLYNOMIAL-RING X, Y, Z, U, W, R, S, T over RATIONAL>
To change the default ring just bind *RING* to whatever you want:
CL-USER> (defparameter *ring*
(make-instance 'polynomial-ring :variables (list 'x 'y))
"QQ[X, Y]")
*RING*
CL-USER> *ring*
#<POLYNOMIAL-RING X, Y over RATIONAL>
Polynomials are defined using a list of terms where each term is a list with the coefficient as its first term and where the remaining elements are variable exponents. For example: (1 1 2 3) would correspond to the term `xy^2z^3`
Thus, to create a polynomial write:
CL-USER> (defparameter *l* (make-polynomial '((1 3 0) (-2 1 1)))) *L* CL-USER> *l* #<POLYNOMIAL x^3 - 2xy> CL-USER> (defparameter *m* (make-polynomial '((3 4 1) (1 2 0)))) *M* CL-USER> *m* #<POLYNOMIAL 3x^4y + x^2>
Use the generic functions RING+, RING-, RING*, and RING/ for the usual arithmetic operations.
The function RING/ is the multivariate polynomial division algorithm and takes a polynomial and a sequence of divisors to produce a sequence of quotients and a remainder.
To set the default monomial ordering, bind *MONOMIAL-ORDERING* to the relevant function (which defaults to LEX>). For example:
CL-USER> (defparameter *monomial-ordering* #'grevlex>) *MONOMIAL-ORDERING*
Also, you can use the macro WITH-MONOMIAL-ORDERING to define the current monomial ordering as in:
CL-USER> (with-monomial-ordering #'grlex>
(ring/ *m* *l*))
#(#<POLYNOMIAL 3xy>)
#<POLYNOMIAL 6x^2y^2 + x^2>
The functions GROEBNER and REDUCED-GROEBNER compute Groebner bases and reduced Groebner bases respectively. Both of them take a sequence of polynomials as parameter. An alternative is to construct a polynomial ideal and obtain its reduced Groebner basis using the BASIS generic function.
For example:
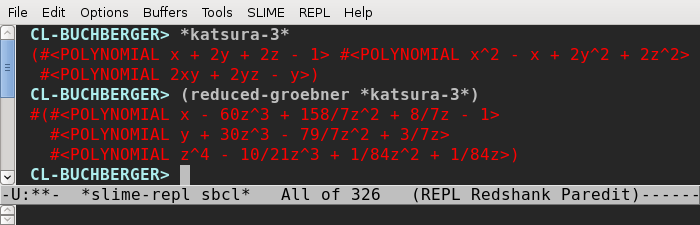
CL-USER> (defparameter *katsura-3*
(make-ideal (list (make-polynomial '((1 1 0 0) (2 0 1 0) (2 0 0 1) (-1 0 0 0)))
(make-polynomial '((1 2 0 0) (-1 1 0 0) (2 0 2 0) (2 0 0 2)))
(make-polynomial '((2 1 1 0) (2 0 1 1) (-1 0 1 0)))))
"Katsura-3 over QQ[x, y, z] (default ring)")
*KATSURA-3*
CL-USER> *katsura-3*
#<IDEAL :RING #<POLYNOMIAL-RING :VARIABLES (X Y Z)
:BASE-FIELD RATIONAL> :GENERATORS #(#<POLYNOMIAL x + 2y + 2z - 1>
#<POLYNOMIAL x^2 - x + 2y^2 + 2z^2>
#<POLYNOMIAL 2xy + 2yz - y>)>
CL-USER> (basis *katsura-3*)
#(#<POLYNOMIAL x - 60z^3 + 158/7z^2 + 8/7z - 1>
#<POLYNOMIAL y + 30z^3 - 79/7z^2 + 3/7z>
#<POLYNOMIAL z^4 - 10/21z^3 + 1/84z^2 + 1/84z>)
There's a bug tracker available at http://github.com/jmbr/cl-buchberger/issues